Cont: UFOs: The Research, the Evidence

[Akhenaten]

I'm just as free to discuss UFOs and whatever I consider to be valid evidence as anyone else here.

And others are free to point out that the UFOs you are discussing aren't the same as the ones everyone else is discussing, and that you don't even know what valid evidence is, let alone have any to present.

You can't even answer the simple question "What is the correct abbreviation for 'Unidentified Flying Object'" so there's no hope of you being able to discuss the rest of the subject with any level of competence.

If you don't like it, you can always ignore it.

That would be considerably easier to ignore if you'd stop spamming the thread with your ridiculous attempts to redefine every second word and yammering on endlessly about your Omgalien religious beliefs.

 

[Sideroxylon]

Mr Ufology, you keep arguing for your definition of UFO as alien through the authority of a superceded definition but you won't/can't address the problem of justification. Care explain how anyone is justified in the leap from "I don't know what I saw" to "I saw a flying saucer"?

 

[23_Tauri]

On This: "... there is simply no way to triangulate the object from the data provided."

If the above is still on the 1953 Point Mugu incident, we have two different angles of view both indicating the bearing as being toward Point Mugu.

"I estimated the position of the object to be roughly over Point Mugu, which lies on a bearing about 255° from my ranch."

"I saw an object apparently standing still in the air off the coast, in the vicinity of Point Mugu"

So in this case we can establish that the 2D intersection point ( x,y ) for the two lines of sight L1 and L2 must is somewhere near Point Mugu, and since the distance from the ground observer to Point Mugu is known, no triangulation is necessary to be able to establish the approximate distance from the object to the ground observer. Simple linear distance measurement is all that is required. It is probable that it is this logic that is being referenced incorrectly with the word "triangulate", a different process that uses trigonometry.

Have you been following the discussion?

The only location for any of the witnesses for which we have any confidence is Johnson, because he was at his ranch. As for the WV-2, we don't know where it was!

A whole six days ago Astrophotographer wrote it quite plainly:

Interesting plot Stray Cat. I find it intersting that none of the witnesses in the WV-2 can seem to agree exactly where the object was located.

Wimmer- East of Santa Cruz island
Thoren-Between Santa Barbara island and Point Mugu
Colman - in the vicnity of Point Mugu (interestingly he states they were off Santa Monica while the others seem to put the plane further south)
Ware-...to the west, over the water, possibly in the vicinity of Santa Barbara Island

The UFOlogists picked a point between Santa Cruz and point Mugu but I think that position is not very accurate and your position seems more correct (possibly a bit further north of Santa Barbara but that is quibbling). One would think these gentlemen could have written down headings of the aircraft and azimuths to provide more precise information.

Since the location of the WV-2 has been one of the main topics of our discussion on the Lockheed case for days now, I am utterly astounded that you haven't noticed this.

In fact, we only have to go back a few hours, to last night (my time) to where Stray Cat gave us a helpful refresher on the vexing problem of the airplane's location (that's the Lockheed one piloted by Thorsen, not your mystery spy plane in the black smoke cloud):

So the Lockheed was in the air for approx 31 minutes before they noticed the object. We know it ended up with a speed of 225mph (but someone more knowledgeable about flying and airspeed whilst climbing to the altitudes mentioned will have more accurate calculations that me) and we know where it took off from.

My rough calculation at the moment tells me that the plane flew between 85 and 100 miles during that time. Taking in account various mentions of heading out "over the ocean" a "South East" direction parallel to the coast and a turn West (that's when they report first noticing the object), that indeed puts the plane in the Catalina Channel. I think this alone rules out the much closer stated point of Coleman who put the plane much further North at Santa Monica.

The other thing is that Although it's the most likely line of sight from Johnson's ranch, directly towards Pt. Mugu to state the object was actually on that line when Johnson couldn't see Mugu from his home because of mountains and was again estimating as we know by his use of "roughly over Point Mugu", perhaps it's wise to also take into account that he mentions two other headings ("between 240° and 260°") as the object "departed". This of course still fit's with the 255° given for Mugu but means that the object could have had a 20° variation from one extreme to the other (that would be the equivalent of being out by 8 miles if the object were 25 miles away and 14.5 miles if the object were 40 miles away etc). this further makes Sparks' claim for triangulation nonsense, whilst maintaining the integrity of the witness (we're not saying Johnson was wrong about any of the factual information he's given).

Indeed, it's proving so tricky to pinpoint the plane's actual location at the time of the sighting that Stray Cat is having to research, and input, data such as the plane's time and location of take-off, speed, altitude and direction over a whole 30 minutes - and then the margins of error taking in account the paucity of the data - in order to get the best estimate of where it was by 4.59pm.

I look forward to his next map and hope we get to see it today. Then you will see exactly how much work is involved in this task. Or not, if you don't pay any attention.

I'm SO demanding!

That you, Mister Ufology, brazenly come charging in with "oh, but triangulation is easy peasy" does nothing except show everyone here that you have no understanding of margins or errors, that you still haven't done one single sum and, if that wasn't damning enough on our resident ufologist, that you haven't even been paying attention to the hard work that others have been doing because you can't be bothered to do it yourself.

As it is, I doubt anyone here needs a lesson from you on how to draw two intersecting lines on a map, two lines that you haven't yet drawn for yourself. What's up? Have you lost your crayons?

 

[Stray Cat]

Astro

Aircraft use magnetic headings/courses almost exclusively. There used to be a system used at the poles, that overlaid a rectangular grid for navigation, but I don''t know if it is still being used. His use of true headings is puzzling to me. And true, maps are laid out with true north on the vertical, but every compass rose on the map shows a magnetic rose, every airport is marked in magnetic and every nav system in the airplane is marked in magnetic. I don't know what is going on with the new gps systems, but if you make a landing, you are landing on a mag course and every airway is marked as magnetic. If you can get a look at a Sectional map, you'' see what I mean.

PD

This little point may have scuppered the work I've been doing on the flight path of the Lockheed from take off somewhat.

When Sparks reads the Lockheed is heading West, he presumes (not without some justification) that the aircrew mean magnetic 285°.
So (and this is the bit that's now confusing me slightly), should we also presume (using the same justification) that when the air crew say they were heading South East (or should that really be 'west' that word is hard to read on the original scan of the report), that they were also reporting that as a magnetic heading (and therefore 150° for South East or 225° for South West )?

I know this is probably an exercise in futility anyway, but so far, from all the sums I've done, the Lockheed would have had to have stopped in mid air for a tea break to be any less further South than Palos Verdes.

 

[Stray Cat]

Stray

I can't give you the real skinny because I don't know the bird, but for a first cut wag try 2/3 of the cruise speed for a recip. So try 150 indicated and 180 true for a TAS average climb speed. Don't trust that very far. No idea what the rate of climb would be and you would need that for time and distance to climb. You would need an old Connie driver or the flight manual for the real stuff.

That 225mph at cruise is going to be the indicated air speed since no one said anything about true airspeed. The TAS at 17-18k altitude should be just under 300 using the 500mb temp at vandenburg.

PD

Thanks.
What I'm trying to do is work out the least amount of distance the Lockheed could have travelled for the amount of time it was in the air (the further it travels away from the object, the bigger that object had to be for them to be able to see it). I'll take your info into account and see where we end up. Much appreciated.

 

[Akhenaten]

This little point may have scuppered the work I've been doing on the flight path of the Lockheed from take off somewhat.

When Sparks reads the Lockheed is heading West, he presumes (not without some justification) that the aircrew mean magnetic 285°.
So (and this is the bit that's now confusing me slightly), should we also presume (using the same justification) that when the air crew say they were heading South East (or should that really be 'west' that word is hard to read on the original scan of the report), that they were also reporting that as a magnetic heading (and therefore 150° for South East or 225° for South West )?

I know this is probably an exercise in futility anyway, but so far, from all the sums I've done, the Lockheed would have had to have stopped in mid air for a tea break to be any less further South than Palos Verdes.

Unless someone has written into a report somewhere in big, red letters that they've converted magnetic headings to true headings and they state their reasons for doing so then yes, assuming magnetic is the way to go.

Aircraft nav systems, especially in the days before GPS, have no way of determining true headings and they would have to be calculated by the aircrew from the magnetic data. In the case of a fast mover the magnetic deviation would have to be recalculated almost continuously - an onerous task with no real benefit since, as PD points out, the things that pilots need to know about like airways, runways etcetera are all laid out in magnetic anyway.

 

[GeeMack]

Mr Ufology, you keep arguing for your definition of UFO as alien through the authority of a superceded definition but you won't/can't address the problem of justification. Care explain how anyone is justified in the leap from "I don't know what I saw" to "I saw a flying saucer"?

It's a religious belief, as he admitted here...

Um ... no ... I haven't rescinded anything. I've only said that so far as I know, we don't have sufficient verifiable scientific evidence to prove my claims or beliefs. But I still believe I've seen an alien craft and I still believe other people have as well ... regardless.

Religion. The same bogus leap of faith that goes like this: "Look at that beautiful sunset, therefore god." No other justification necessary.

 

[remirol]

Um ... no ... I haven't rescinded anything. I've only said that so far as I know, we don't have sufficient verifiable scientific evidence to prove my claims or beliefs.

This is where logical, honest people stop and say "Therefore, there is no reason to believe that alien craft exist." This is why people do not believe witches exist -- there is no evidence that they do.

But I still believe I've seen an alien craft and I still believe other people have as well ... regardless.

And this is where you head straight off the logic trails and deep into the wilderness of Wishful Thinking, Hope, Faith, and Selling Sensationalism To Suckers. That last one is why you're getting such a hostile reception here, by the way.

See, judging by your website, you have a financial interest directly related to the latter -- even though there is no evidence for aliens, you need to keep up the pretense so that people will track back to your site and buy things through your links. This is what we call a "scam".

Fortunately, this and the prior thread are now tracking very highly in Google, so anyone who does a token amount of research will see this and know that, in fact, there was never any evidence for alien craft presented in this thread. There's always a subsection of the population which can be fooled, and there's no point worrying about who's taking that subsection's money -- someone always is. The goal of ensuring that more responsible people don't fall for it, though, is being met quite nicely.

 

[Stray Cat]

Thanks Akhenaten

I've put that to one side for now until I can get round to doing some more sums regarding speed/TAS and stuff, but may come back to it this afternoon.


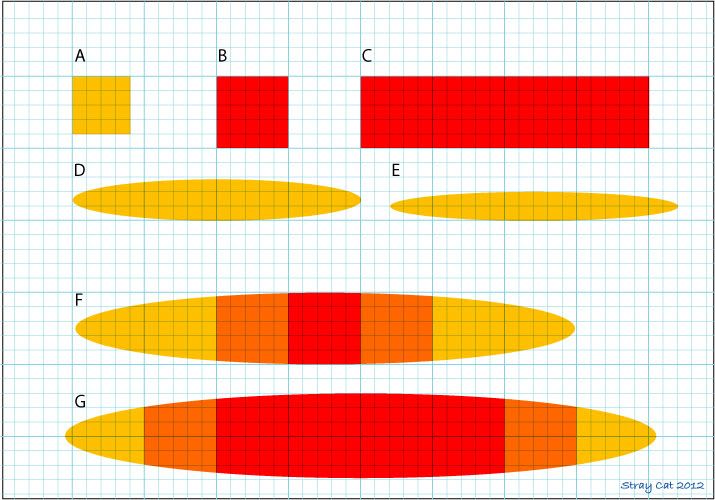
For now, I've been looking at this minimum resolution the human eye can resolve and would like to know from anyone if I'm understanding this correctly. So I've done a helpful diagram to explain it the way I understand it.

Each 5x5 square represents 1 arc minute.

Yellow = Impossible to resolve
Orange = May just be possible to resolve
Red = Can be resolved

A: It is impossible for the eye to see anything that is less than 1 arc minute so anything with an angular size this big can not be seen.

B: This is the absolute smallest unit that can be seen by the human eye (presuming 20/20 vision)

C: An object 4 arc minutes wide would look like this, presuming it was made up of 4 blocks each 1 arc minute square.

D: Sparks calculates the object to have been 4 arc minutes wide and Johnson describes the object as being an ellipse with a dimension between 7:1 and 10:1. If the object is simply 4 arc minutes across and 7:1, it is only 0.54 arc minutes in height and therefore can't be seen because it doesn't fit the criteria of being the minimum 1 arc minute that the eye can see.

E: The same as C only with an ellipse which is 10:1.

F: Using only the 7:1 ellipse (that's the most forgiving one in relation to Sparks' calculations), for anything to be seen the object must have been at least 1 arc minute in height, which makes it a lot wider than 4 arc minutes across. Using Sparks' calculations that an object 4 arc minutes would be 200' wide, we can see that even at it's minimum resolution, the object would be 7 arc minutes across, which would make it 350' wide (31' wider than the wingspan of the Spruce Goose).

G: For the ellipse of 7:1 to be 4 arc minutes wide and still be resolvable by the human eye, each of those arc minutes must be at least 1 arc minute in height. So to get an area within the ellipse that is at least 1 arc minute high for at least 4 arc minutes across we see the shape has to further increase in size to 8.2 arc minutes wide and 1.2 arc minutes high (at it's maximum). Again using Sparks' 4 arc minutes as being 200' wide, the ellipse would have to be over 400' wide to be resolved as a 4 arc minute wide object.

Am I correct with this or am I misunderstanding it?

 

[RoboTimbo]

Um ... no ... I haven't rescinded anything. I've only said that so far as I know, we don't have sufficient verifiable scientific evidence to prove my claims or beliefs. But I still believe I've seen an alien craft and I still believe other people have as well ... regardless.

And it's ok to believe in your religion without evidence. You shouldn't let the irrationality of that keep you from the free exercise of worshipping your god(s), the OMGaliens. We've been teasing you with UFOs ( witches ) because they are just a different version of The Flying Spaghetti Monster. You played the part of the martyred believer to the hilt. Thanks!

Would you like me to ask the mods to move this to the religion sub-forum for you?

 

[R.A.F.]

Would you like me to ask the mods to move this to the religion sub-forum for you?

Since [ufology] freely admits the only thing he has is his belief, the religion forum is EXACTLY where this thread belongs.

Edited by kmortis: 

Removed personal comment

..but I suggest not holding your breath waiting for it to get moved there...

 

[Astrophotographer]

Astro

Aircraft use magnetic headings/courses almost exclusively. There used to be a system used at the poles, that overlaid a rectangular grid for navigation, but I don''t know if it is still being used. His use of true headings is puzzling to me. And true, maps are laid out with true north on the vertical, but every compass rose on the map shows a magnetic rose, every airport is marked in magnetic and every nav system in the airplane is marked in magnetic. I don't know what is going on with the new gps systems, but if you make a landing, you are landing on a mag course and every airway is marked as magnetic. If you can get a look at a Sectional map, you'' see what I mean.

PD

Hmmm...That is interesting to say the least. However, when describing the direction one was heading, the pilot just stated:

We continued our climb in a south-easterly direction and somewhere in the vicinity of Long Beach or Santa Ana between 16,000 and 20,000 feet we made a right turn onto a west heading.

Are we led to conclude that this was magnetic west or true west? That is the issue here.

 

[Astrophotographer]

"I saw an object apparently standing still in the air off the coast, in the vicinity of Point Mugu"

However, that is not what all the witnesses stated. You have to remember, these statements were written AFTER talking to Kelly Johnson, who told them he saw the same thing in the direction of Point Mugu. Exactly how much influence did it have on the person that wrote this? This was also the person who stated they were flying off of Santa Monica, while the others put themselves closer to Long Beach and Santa Catalina.

Meanwhile, the others gave more vague location

"somewhere east of Santa Cruz island" (and this was for the cloud layer he saw and not the specific object)
"It’s direction was almost due west"
"I had estimated that it was somewhere between Point Mugu and the Santa Barbara Islands."
"It seemed to be somewhat above us and to the West, over the water, possibly in the vicinity of Santa Barbara Islands."

As I said, one has to wonder how much influence that Johnson's statement had over them prior to them writing their statements.

 

[GeeMack]

[* Visibility analysis snipped. *]

Am I correct with this or am I misunderstanding it?

It looks like a good analysis to me. So if the object was only 200 feet wide, about the maximum of any conceivable aircraft that might have been flying at that time and place, Kelly Johnson couldn't have even seen it without the binoculars. And if he didn't even see it without the binoculars, he certainly wouldn't have requested the binoculars to get a better look.

But benefit of the doubt and all that, even with 8X binoculars, the scene would have only looked something like this...

Again, to get that into a human perspective, hold a tennis ball at arm's length, step away from your computer monitor until that tennis ball just fits within the black circle, then move the tennis ball aside. That is an approximation of Kelly Johnson's view of a 200 foot wide plane with wings about 30 feet thick! There's also my other real-life example of seeing a 200 foot wide 747 at 6 to 8 miles in the air, making it 3 or 4 times further away and hence smaller, and getting rid of the contrail so you don't have a huge visible pointer. It's pretty clear, quantitatively and objectively, that Johnson was not seeing any sort of aircraft.

So ufology's conclusion in this case is drawn from exactly the same religious faith as his claim that some UFOs are alien craft. But no, proper as it may be, I don't think we can expect this thread to be moved to the religion and philosophy category now, even though he's admitted all his belief in aliens is just like a religion to him.

 

[Astrophotographer]

Thanks.
What I'm trying to do is work out the least amount of distance the Lockheed could have travelled for the amount of time it was in the air (the further it travels away from the object, the bigger that object had to be for them to be able to see it). I'll take your info into account and see where we end up. Much appreciated.

One also has to consider the wind speed at that altitude when computing the true air speed. As best I can tell, the winds were coming from a bearing of about 293 and a speed of about 30 knots (so the plane would essentially be flying into the wind). That data is from Long Beach and was two hours after the event. One can assume that it was about the same at the time of the sighting.

 

[lancemoody]

@Straycat:

Thanks for pointing out the difficulty in reading the Bluebook file.

I also struggled with the "southeast" or "southwest" wording.

There used to be several versions of the files online, including a redacted one. All of those but one seem to now be offline.

When I was doing my transcriptions, I blew up this section very large on my 30" monitor and compared the different versions. I finally decided on southeast but admit that there is some room for error.

When I first posted my transcripts, I asked for corrections but never received any. Now since I look at it again I see several typos which I have corrected in my master file. If anyone has corrections or other opinions on these matters, I would be happy to hear them.

@Stray Cat: nice work. Where does our reliance that the human eye can only resolve above 1 arc minute come from? Hopefully not just from Sparks?

@Tim, in regards to the weather data, I called a meteorologist at a station on the coast (can't remember exactly where but quite near Point Mugu) when I was looking into this. I was mainly inquiring if lenticulars were known in the area (they were). I remember that he told me that things change rapidly there as the sun goes down--this ties in with my evaporating cloud idea, I think. It may be that data from two hours later is not reliable, I don't know this for sure.

I'm not as technically-minded about these things and probably asked the wrong questions when I called out there.




Best,

Lance

 

[Sideroxylon]

Since [ufology] freely admits the only thing he has is his belief, the religion forum is EXACTLY where this thread belongs.

Edited by kmortis: 

Removed personal comment

..but I suggest not holding your breath waiting for it to get moved there...

No, not with all the quality research into UFO (Unidentified Flying Object) sightings provided by some of our forum members. Hats off to you all. I hope you choose to examine new cases to see where the evidence goes.

 

[Astrophotographer]

When Sparks reads the Lockheed is heading West, he presumes (not without some justification) that the aircrew mean magnetic 285°.
So (and this is the bit that's now confusing me slightly), should we also presume (using the same justification) that when the air crew say they were heading South East (or should that really be 'west' that word is hard to read on the original scan of the report), that they were also reporting that as a magnetic heading (and therefore 150° for South East or 225° for South West )?

I know this is probably an exercise in futility anyway, but so far, from all the sums I've done, the Lockheed would have had to have stopped in mid air for a tea break to be any less further South than Palos Verdes.

This is an assumption that we can not conclude as what actually happened.The pilot may have flown on a bearing of 255, and understanding the magnetic deviation, knew he would be flying in a true west direction? Stating he was absolutely flying in a magnetic west direction is making an assumption that may or may not be correct.

 

[Astrophotographer]

I finally decided on southeast but admit that there is some room for error.

The redacted one appears to read southest. I don't think it is that important since it only indicates where the plane headed after takeoff. It gives a general location as to where they made the turn towards the west.

 

[Stray Cat]

It looks like a good analysis to me. ...

Thanks, I was just wondering if I had somehow overlooked something about this minimum resolution.
Seems not.

So ufology's conclusion in this case is drawn from exactly the same religious faith as his claim that some UFOs are alien craft. But no, proper as it may be, I don't think we can expect this thread to be moved to the religion and philosophy category now, even though he's admitted all his belief in aliens is just like a religion to him.

I'll point out for ufology's benefit (and anyone else who may get the wrong impression), I'm not trying to debunk either ufology or Sparks here.
I'm actually trying to mathematically confirm them.
Sadly, it seems that I can't. In fact the numbers appear to show that they are both wrong.