Probability of a probability being wrong?

[copterchris]

Not knowing the answer to this has bugged me for ages...

If an event is hypothesized to have probability x, how many observations of the event not happening does it require to invalidate the hypothesis, or of being confident that 'x' is wrong?

e.g. I hypothesize that there is a 1 in 100 of an earthquake in a given year, how many years of no earthquakes would it take before I could be confident that 1:100 is not correct

 

[theprestige]

At least a hundred years.

Generally, I guess you'd just watch your sample data accumulate, and see if the data points converge on your predicted probability line. If they do, great! If they diverge, then your prediction is probably wrong. Either way, the more data points you collect, the more confident you can be.

But I am not a mathematician. Basically this is just a placeholder until somebody comes along with error bars and sigmas and trembalos and whatnot.

 

[marplots]

Not knowing the answer to this has bugged me for ages...

If an event is hypothesized to have probability x, how many observations of the event not happening does it require to invalidate the hypothesis, or of being confident that 'x' is wrong?

e.g. I hypothesize that there is a 1 in 100 of an earthquake in a given year, how many years of no earthquakes would it take before I could be confident that 1:100 is not correct

You have to put a number on the word "confident." Otherwise, you can't measure it with the same ruler. Right now, your question is equivalent to:
"How many years of no earthquakes until I can say that earthquakes are amazing?"

Once you put a scale on what "confidence" means, you'll start to get answers in terms of other probabilities, something like, "There is only a 5% chance that my original probability was correct," or "If my hypothesis is correct, I'd only expect to see these results once in a thousand repetitions of the experiment."

 

[jt512]

Not knowing the answer to this has bugged me for ages...

If an event is hypothesized to have probability x, how many observations of the event not happening does it require to invalidate the hypothesis, or of being confident that 'x' is wrong?

e.g. I hypothesize that there is a 1 in 100 of an earthquake in a given year, how many years of no earthquakes would it take before I could be confident that 1:100 is not correct

Zero years. The probability that .01 is the exact probability is 0. After all, it would be contradicted if the true value were .011, or .0101, or .01000001, etc. You need to refine your question. Perhaps specify an interval.

 

[ddt]

Not knowing the answer to this has bugged me for ages...

If an event is hypothesized to have probability x, how many observations of the event not happening does it require to invalidate the hypothesis, or of being confident that 'x' is wrong?

e.g. I hypothesize that there is a 1 in 100 of an earthquake in a given year, how many years of no earthquakes would it take before I could be confident that 1:100 is not correct

So you have two hypotheses:
1) the null hypothesis: the probabilitty of an earthquake happening in a year is 0.01
2) the alternative hypothesis: that probability is lower.

Your basic assumption is the null hypothesis, which you only reject in favour of the alternative hypothesis if the observations don't jive with the null hypothesis.

Choose you significance level α , i.e., how confident do you want to be that you rightly reject the null hypothesis? In fact, α is the probability (under the null hypothesis) that the observations occur. Typical values for α are 0.05, 0.01, and smaller. The smaller α , the smaller the chance of a type I error, that you wrongly reject the null hypothesis.

The probability of no earthquake happening in n subsequent years, under the null hypothesis, is simply: ( 1 - 0.01 ) ^ n = 0.99 ^ n

So, for your chosen α, solve the inequality

0.99 ^ n < α

and you're done.

 

[jt512]

So you have two hypotheses:
1) the null hypothesis: the probabilitty of an earthquake happening in a year is 0.01
2) the alternative hypothesis: that probability is lower.

Your basic assumption is the null hypothesis, which you only reject in favour of the alternative hypothesis if the observations don't jive with the null hypothesis.

Choose you significance level α , i.e., how confident do you want to be that you rightly reject the null hypothesis? In fact, α is the probability (under the null hypothesis) that the observations occur. Typical values for α are 0.05, 0.01, and smaller. The smaller α , the smaller the chance of a type I error, that you wrongly reject the null hypothesis.

The probability of no earthquake happening in n subsequent years, under the null hypothesis, is simply: ( 1 - 0.01 ) ^ n = 0.99 ^ n

So, for your chosen α, solve the inequality

0.99 ^ n < α

and you're done.

So let's say that I observe no earthquakes for 300 years. What is the probability that the true (annual) earthquake probability is less than .01?

 

[psionl0]

So let's say that I observe no earthquakes for 300 years. What is the probability that the true (annual) earthquake probability is less than .01?

There is not enough information to make that determination.

For a small probability of success like that you would need something like 10,000 years to estimate a probability of an earthquake. Assuming that 1% is the probability then the mean number of earthquakes observed would be 100 with a standard deviation of 10 years.

IOW if you observed 100 earthquakes in 10,000 years then assuming a 95% confidence interval (+2 standard deviations) you would estimate the probability of an earthquake to be between 0.8% and 1.2%.

 

[ddt]

So let's say that I observe no earthquakes for 300 years. What is the probability that the true (annual) earthquake probability is less than .01?

Can't say. But I can say the following:

Premise: suppose the probability of an earthquake happening in a year is 1%.
Then the probability of no earthquake happening for 300 years is 4.9%.

It's up to you how much confidence you want to have in rejecting the premise. If you take your α as 0.05, you reject the premise. If you take a smaller α, you don't.

 

[Modified]

Any confidence level you compute will be wrong if earthquakes are not randomly distributed over time.

Earthquakes are not randomly distributed over time.

I'm not sure how far they are from random. It may be close enough for government work.

 

[psionl0]

So let's say that I observe no earthquakes for 300 years. What is the probability that the true (annual) earthquake probability is less than .01?

Here is an alternative view:

If zero earthquakes in 300 years is to be within the 95% confidence interval then we require the standard deviation to be half the mean number of earthquakes in 300 years.

Since mean = 300p
and SD = SQRT(300p) (assume that q = 1-p = 1)
That means that SQRT(300p) = 0.5*300p
for which the solution is p = 4/300 or p = 1.33%

ie the probability that an earthquake occurs in any year must be less than 1.33%.
I suppose that the probability being less than 0.01 given that it is less than 0.0133 is 3/4.

Earthquakes are not randomly distributed over time.

Don't be a spoil sport.

 

[edd]

Hypothesis testing doesn't yield the probability of a hypothesis being wrong.

 

[ddt]

Here is an alternative view:

If zero earthquakes in 300 years is to be within the 95% confidence interval then we require the standard deviation to be half the mean number of earthquakes in 300 years.

The two sigma rule for a 95% confidence internval is (more or less) right with the normal distribution. But this is the binomial distribution, with a small p, so this approximation is not going to work.

Since mean = 300p
and SD = SQRT(300p) (assume that q = 1-p = 1)

Yes, actually it is: SD = sqrt ( 300 * p * (1-p) )

That means that SQRT(300p) = 0.5*300p
for which the solution is p = 4/300 or p = 1.33%

ie the probability that an earthquake occurs in any year must be less than 1.33%.

This online calculator, which uses an exact method, gives p < 0.01222 , IOW, p < 1.22% .

I suppose that the probability being less than 0.01 given that it is less than 0.0133 is 3/4.

Now you're somehow assuming that the a priori probability of earthquakes is in itself a stochast with a uniform distribution?

 

[psionl0]

The two sigma rule for a 95% confidence internval is (more or less) right with the normal distribution. But this is the binomial distribution, with a small p, so this approximation is not going to work.

It's not so much that it won't work but that the answer is going to be rough - especially since p is so much less than 1/2.

Using a spreadsheet and a cumulative binomial distribution with 300 trials, I find that if P(0 < X < 6) = 0.95 then p = 0.011001 so my quick pencil and paper calculation was in the right ball park.

Of course you could argue that a 91% probability that p < 0.01 doesn't look anything like 75% but getting a reliable number from information as limited as "zero earthquakes in the last 300 years" is more of a guess than anything else anyhow.

Now you're somehow assuming that the a priori probability of earthquakes is in itself a stochast with a uniform distribution?

Why not? "p" is a rubbery number to begin with and nothing about the information supplied suggests a favoured value for p.

 

[jt512]

Here is an alternative view:

If zero earthquakes in 300 years is to be within the 95% confidence interval then we require the standard deviation to be half the mean number of earthquakes in 300 years.

Since mean = 300p

I assume that p here is the probability that a year has an earthquake. Then p is the mean. 300p is the total number of years that have earthquakes, which equals the total number of earthquakes, assuming no year has more than one.

and SD = SQRT(300p) (assume that q = 1-p = 1)

So, you're trying to calculate the SD of the total number of earthquakes in 300 years (or more precisely, the number of years that have earthquakes). Assuming that the years are a collection of 300 bernoulli trials, the SD of the total number of earthquakes would be sqrt(300p(1-p)). I guess your parenthetical note, above, is supposed to mean that you're ignoring 1–p, since it's close to 1, and not that p=0, which is what it actually implies.

That means that SQRT(300p) = 0.5*300p
for which the solution is p = 4/300 or p = 1.33%

ie the probability that an earthquake occurs in any year must be less than 1.33%.

OK. After considerable struggle, I think I understand what you've done. You're modelling the number of years that have earhquakes as Binomial(n,p), and then using the normal approximation to the binomial to determine p such that the lower limit of the 95% CI for p is 0. (Why didn't you just say so!) And you've determined that p to be about 1.33%. Thus, in a 95% confidence sense, observing 0 earthquakes in 300 years is consistent with any annual earthquake probability less than 1.33%

It follows from your logic that observing 0 earthquakes in 300 years is not sufficient evidence to say that the true annual probability is less than 1%. However, this does not give us the probability that the true annual earthquake risk is < 1.33% given that we've observed 300 earthquake-free years.

I suppose that the probability being less than 0.01 given that it is less than 0.0133 is 3/4.

That is bad logic facilliated by sloppy wording. First of all, the fact that the 95% CI includes 0 earthquakes (in 300 years) if and only if the true annual earthquake risk is less than 1.33% does not even remotely imply that the true risk "is" less than 1.33%, or in other words that the probability is 1 that the true risk is less than 1.33%. Therefore, it makes no sense to take the next step and assume that the probability that the true risk is less than T is equal to T/1.33.

 

[psionl0]

This online calculator, which uses an exact method, gives p < 0.01222 , IOW, p < 1.22% .

I originally thought your on-line calculator used the normal distribution without the q=1 approximation. However it is actually a correct use of the binomial distribution in this instance. (My 2am calculation was flawed because it assumed that the mean number of earthquakes in 300 years was 3 - something I was meant to prove).

One could also use an exponential distribution to calculate the mean time between earthquakes given a 95% confidence interval but it wouldn't improve original calculation by much - especially given the closeness of 1.33% to the "correct" figure of 1.22%.

That is bad logic facilliated by sloppy wording. First of all, the fact that the 95% CI includes 0 earthquakes (in 300 years) if and only if the true annual earthquake risk is less than 1.33% does not even remotely imply that the true risk "is" less than 1.33%, or in other words that the probability is 1 that the true risk is less than 1.33%. Therefore, it makes no sense to take the next step and assume that the probability that the true risk is less than T is equal to T/1.33.

Actually, it was a very carefully worded conclusion - IF the probability of an earthquake is less than 1.33% THEN . . . .

Obviously, you could have zero earth quakes in 300 years even if the probability of an earthquake in one year was considerably greater than 1.33%. It just illustrates what I stated earlier that 300 years is far too small a sample size to draw any meaningful conclusions about the probability of an earthquake in any one year (or the mean time between earthquakes if you wanted to be more accurate).

 

[jt512]

ie the probability that an earthquake occurs in any year must be less than 1.33%.
I suppose that the probability being less than 0.01 given that it is less than 0.0133 is 3/4.

That is bad logic facilitated by sloppy wording. First of all, the fact that the 95% CI includes 0 earthquakes (in 300 years) if and only if the true annual earthquake risk is less than 1.33% does not even remotely imply that the true risk "is" less than 1.33%, or in other words that the probability is 1 that the true risk is less than 1.33%. Therefore, it makes no sense to take the next step and assume that the probability that the true risk is less than T is equal to T/1.33.

Actually, it was a very carefully worded conclusion - IF the probability of an earthquake is less than 1.33% THEN . . . .

From your analysis it does not follow that the probability of an earthquake is less than 1.33% (even probabilistically), and even if you assume that the probability is less than 1.33%, it does not follow that the conditional probability of it being less than 1% is .75.

It just illustrates what I stated earlier that 300 years is far too small a sample size to draw any meaningful conclusions about the probability of an earthquake in any one year (or the mean time between earthquakes if you wanted to be more accurate).

The OP asked how many consecutive years without an earthquake would need to be observed in order to confidently reject the hypothesis that the annual risk of earthquake was 1%. The implied alternative hypothesis is that the earthquake risk is less than 1%. You illustrated (in an earlier post) that in order to get a reliable estimate of the annual earthquake risk something on the order of 10,000 years of data would be required. However, answering the OP's question does not require estimating the true earthquake risk. We would need only enough earthquake-free years to reject the 1% hypothesis. This can be done with far fewer than 10,000 years of data. The precise number of years needed depends on how we define the alternative hypothesis, that is, the probability distribution of the true risk under the hypothesis that it is less than 1%. A Bayesian analysis can give a sensible answer to this type of question. I'll try to elaborate in a subsequent post.

 

[psionl0]

Here is an alternative view:

If zero earthquakes in 300 years is to be within the 95% confidence interval then we require the standard deviation to be half the mean number of earthquakes in 300 years.

Since mean = 300p
and SD = SQRT(300p) (assume that q = 1-p = 1)
That means that SQRT(300p) = 0.5*300p
for which the solution is p = 4/300 or p = 1.33%

ie the probability that an earthquake occurs in any year must be less than 1.33%.
I suppose that the probability being less than 0.01 given that it is less than 0.0133 is 3/4.

From your analysis it does not follow that the probability of an earthquake is less than 1.33% (even probabilistically)

That's how much of my post you would have to cross out to make that strawman argument. Even just including the bolded bit would make your statement a non-sequitur.

 

[jt512]

I hypothesize that there is a 1 in 100 [chance] of an earthquake in a given year, how many years of no earthquakes would it take before I could be confident that 1:100 is not correct

The wording of your question implies that you want to test the "null" hypothesis that the annual risk of an earthquake occurring is 1% vs. the alternative hypothesis that the annual risk of an earthquake is less than 1%. You want to know how many consecutive earthquake-free years you would need to observe in order to confidently conclude that the true risk is less than 1%.

Your question can be answered by using Bayesian statistics. The precise answer will depend on how you formulate the alternative hypothesis. That is, if the alternative hypothesis is true—if the true risk is less than 1%—how plausible are various values for the true risk. Do you think all values less than 1% are equally plausible, or do you have, for instance, reason to believe that values closer to 1% are more likely to be true than values close to 0? I'll do the calculations for two such alternative hypotheses. In both cases the null hypothesis, H0, is the same: the annual risk, p, is .01. These two tests will be as follows:

Test 1 will be

H₀: p = .01 vs.
H₁: p < .01, with all values between 0 and .01 considered equally plausible (ie, uniformly distributed).

Test 2 will be

H₀: p = .01 vs.
H₂: p < .01, with the plausibility of p decreasing as p gets further away from .01. We'll represent our belief about the plausibility of various values of p under H₂ by using the distribution depicted below, which is the portion of a normal distribution whose mean is .01 and whose standard deviation is .01/3, that lies between 0 and .01 (renormalized so that it integrates to 1).

​

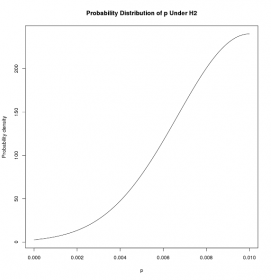
The result of each test will be a Bayes factor (BF), defined as

BF_A = P(D|H_A) / P(D|H₀) ,​

where D is our data, the number of consecutive years, N, of no earthquakes; H_A will either be H₁ or H₂; and P stands for "probability." Let's say we choose N to be 300 years. Then, the expression P(D|H₁) would mean the probability of 300 consecutive years of no earthquakes under hypothesis H₁, and P(D|H₀) would mean the probability of 300 consecutive years of no earthquakes under the null hypothesis of 1% per year risk. Thus, the Bayes factor is the ratio of the probabilty of the data under two competing hypotheses about the annual earthquake risk. The larger the Bayes factor, the more the data favor the alternative hypothesis over the null. For example, BF=100 would mean that the data is 100 times more likely under the alternative possible than under the null.

The general formula for our Bayes factor is

,​

where dbinom(0, N, p) is the binomial probability of 0 earthquakes in N consecutive years if the probability of an earthquake is p each year, and f_A(p) is the probability density function of p under the alternative hypothesis: uniform for H₁, and the half-normal density discussed above for H₂.

The denominator of BF_A, P(D|H₀), is easy to deteermine. The numerator, P(D|H_A), is more difficult. It is basically a weighted average of the probability of the data under the particular alternative hypothesis, where the weights are the values of f_A(p), the distribution of p under the appropriprate alternative hypothesis. Since both the uniform and half-normal distributions are continuous, we have to integrate to calculate this average.

Results for H₁​

The Bayes factors for N=300, 600, 900, and 1000 years are, respectively, 6.4, 69, 940, and 2314. Thus, for instance, observing 600 consective years without an earthquake favors the alternative hypothesis, that the true annual earthquake risk is less than 1%, over the null hypothesis, that the risk is 1%, by a factor of 69. That is, the data are 69 times more likely under the alternative hypothesis than the null. Recall that our assumption about the alternative hypothesis was that all values less than 1% are equally likely.

Results for H₂​

The Bayes factors for N=300, 600, 900, and 1000 years are, respectively, is 2.7, 12, 94, and 200. As in Test 1, the data favor the alternative hypothesis over the null, but not as strongly. This is because an observation of zero earthquakes, which suggests an annual risk close to zero, is less compatible with the half-normal distribution, which favors p's nearer to 1, than with the uniform distribution of Test 1, which considers all values of the risk less than .01 equally likely.

So, the bottom line is that you can get strong evidence against the null that the annual risk is 1% with serveral hundred years of data consisting of no earthquakes. How many years of data depends on your beliefs about the annual risk of an earthquake under the hypothesis that the risk is less than 1%.

I hope that was understandable.

 

[jt512]

From your analysis it does not follow that the probability of an earthquake is less than 1.33% (even probabilistically)

That's how much of my post you would have to cross out to make that strawman argument. Even just including the bolded bit would make your statement a non-sequitur.

Really? OK. Based on your analysis, what is the probability that the true risk of an earthquake is less than 1.33%?

 

[Floyt]

[Bayes]